 |
|
 |
|

Die Effizienz, mit der numerische Methoden auf Rechnersystemen implementiert werden, hängt entscheidend von den verwendeten Werkzeugen ab. Eine an der mathematischen Notation orientierte Schreibweise spielt dabei eine wichtige Rolle. Ein weiterer wichtiger Punkt ist die Unterstützung des gesamten Entwicklungsprozesses. Nur so kann ein Sprachwechsel beim Übergang von der Entwicklungs- zur Produktionsphase vermieden werden.
Die an diesem Arbeitsbereich entwickelte Programmiersprache COX erweitert die Sprache C um ein allgemeines Operatorkonzept. Dieses ermöglicht eine stark an der mathematischen Notation orientierte Programmierung. Darüber hinaus ist COX sowohl kompilativ als auch interpretativ nutzbar.
einfache Syntax |
umfangreiche Standardbibliotheken |
||
Benutzen der gewohnten mathematischen Operatoren |
integriertes Hilfesystem |
||
kombinierter Präcompiler und Interpreter |
beliebig erweiterbar, da aufwärtskompatibel zu C |
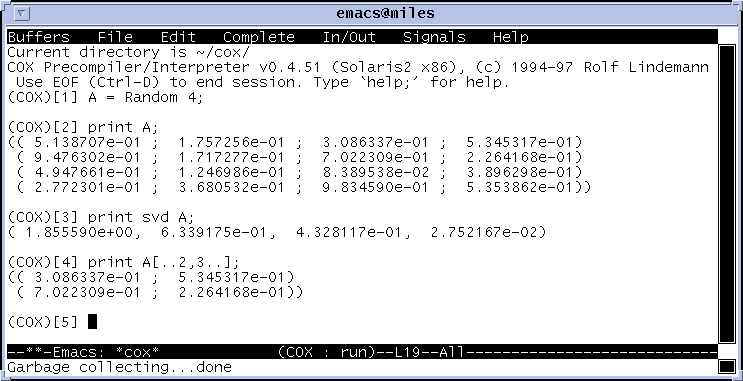
einfache Bedienung aus dem Editor |
intuitive Schreibweise
einfacher Zugriff, auch auf Unterbereiche
durch das allgemeine Operatorkonzept lassen sich auch Funktionen mit mehreren Ergebnissen auf natürliche Weise aufrufen
Der integrierte Präcompiler erzeugt aus Ihrem Code blitzschnelle Programme. Änderungen an dem Algorithmus sind dazu nicht notwendig.
Kommentare werden automatisch aus dem Quelltext extrahiert. Hieraus kann dann eine Online-Hilfe (Texinfo und HTML) sowie die gedruckte Dokumentation (TeX) generiert werden
Kommentare im Quelltext
Der modulare Aufbau des COX Systems sichert die Portabilität. Klar definierte Schnittstellen ermöglichen eine gute Integration von externen Komponenten, wie z.B. Editor oder 3D Grafik Programmen.
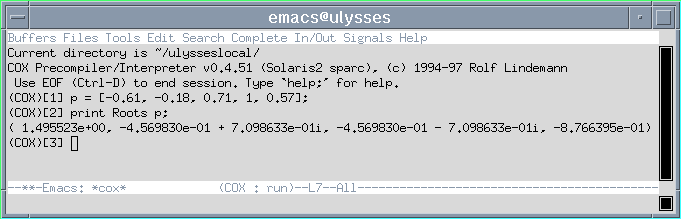
Um z.B. die Nullstellen des Polynoms p(x) = -0.61*x4-0.18*x3+0.71*x2+x+0.57 zu bestimmen, kann in COX die Funktions Roots benutzt werden. Die Koeffizienten des Polynoms müssen dazu in einen Vektor (in diesem Beispiel p) geschrieben werden.
Viele Verfahren zur Bestimmung von Nullstellen basieren auf dem Newton-Verfahren. Nachfolgendes Java-Applet demonstriert seine Arbeitsweise grafisch.
Lokale Nullstellensuche mit dem Newton-Verfahren
Ein Klick mit der linken Maustaste erzeugt ein neues, zufälliges
Polynom und startet die Nullstellensuche.
Ein Klick mit der rechten Maustaste startet die Nullstellensuche erneut
(ohne das Polynom zu verändern).
Umschalt+ linke Maustaste setzt den Startwert (x0) neu.
Steuerung+ Maustaste zoomt den Bereich.
Umschalt+Steuerung+ Maustaste verändert die Geschwindigkeit.
Der rote Kreis markiert den aktuellen Iterationspunkt, die blaue Linie
ist die Tangente an diesem Punkt. Die grüne Linie markiert die Nullstelle
der Tangente und damit den nächsten Iterationswert.
Die Java Quelldateien
Ein zweites Beispiel soll die Berechnung von Ableitungen einer Funktion an einer gegebenen Stelle sein, hier f(x) = eSin x1*Cos x2 an der Stelle x1=3 und x2=4.
Dazu wird als erstes der Vektor x definiert, dann die Variable, nach der abgeleitet werden soll festgelegt. Danach muß nur noch die Funktion selbst eingegeben werden. In der Variablen yg steht danach sowohl der Funktionswert an der entsprechenden Stelle, als auch der Wert der Ableitung.
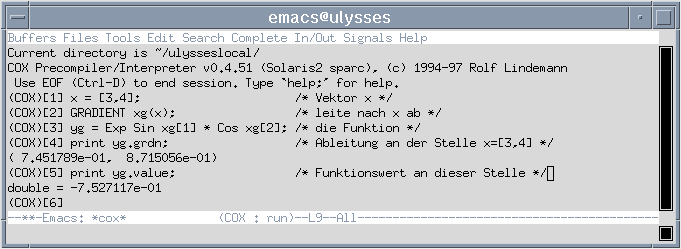
Das hier verwandte Verfahren zur Berechnung der Ableitung benutzt weder den symbolischen Ausdruck der Ableitung noch eine Näherung z.B. durch Differenzenquotienten. Die Ableitung wird an einer konkreten Stelle präzise und automatisch berechnet.
Rolf Lindemann, Technische Universität Hamburg-Harburg
Email: Lindemann@tu-harburg.de