DEMOHESSIAN Short demonstration of Hessians

Contents

Some sample applications of the Hessian toolbox

Hessians implement second order automatic differentiation in forward mode.

format compact long _
setround(0)                           % set rounding to nearest

Initialization of Hessians

The initialization follows the same principles as for gradients, for example

x = hessianinit([ -.3 ; pi ])

Hessian value x.x = 
  -0.300000000000000
   3.141592653589793
Hessian derivative(s) x.dx = 
     1     0
     0     1
Hessian second derivative(s) x.hx(1,1,:,:) = 
     0     0
     0     0
Hessian second derivative(s) x.hx(2,1,:,:) = 
     0     0
     0     0

Access of the Hessian

Define the function f: R^n->R^n by

f = @(x)( 3*x(1)*x + sin(x).*(sec(x)-sqrt(x)) )

f =
  function_handle with value:
    @(x)(3*x(1)*x+sin(x).*(sec(x)-sqrt(x)))

The number of unknowns is determined by the length of the input vector x. For example,

f(1:4)

ans =
  Columns 1 through 3
   3.715936739847006   2.529019383490645   8.613026433001503
  Column 4
  14.671426272965434

The function can be evaluated using the Hessian package as follows:

y = f(hessianinit([1.1 -2.7 pi]'));

There is direct access of the Hessian of y=f(x) by

y.hx

ans(:,:,1,1) =
 25.793906481681820 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
ans(:,:,2,1) =
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
ans(:,:,3,1) =
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
ans(:,:,1,2) =
  0.000000000000000 + 0.000000000000000i
  3.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
ans(:,:,2,2) =
  3.000000000000000 + 0.000000000000000i
  1.156737479094823 - 1.276540468064363i
  0.000000000000000 + 0.000000000000000i
ans(:,:,3,2) =
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
ans(:,:,1,3) =
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
  3.000000000000000 + 0.000000000000000i
ans(:,:,2,3) =
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
ans(:,:,3,3) =
  3.000000000000000 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i
  0.564189583547756 + 0.000000000000000i

However, y.hx contains the Hessians of all three component functions of the original function f. To access the Hessians it is recommended to use the Hessian of individual components, not components of y.hx:

H3 = y(3).hx

H3 =
                   0                   0   3.000000000000000
                   0                   0                   0
   3.000000000000000                   0   0.564189583547756

The matrix H3 is the Hessian of the third component function of f at x.

A simple example

Consider the following function

f = inline(' sin(x-log(x+2))-x*cosh(x)/15 ')

f =
     Inline function:
     f(x) = sin(x-log(x+2))-x*cosh(x)/15

To plot the function first vectorize f :

F = vectorize(f)

F =
     Inline function:
     F(x) = sin(x-log(x+2))-x.*cosh(x)./15

Plot the function including the x-axis:

x = linspace(-1,3); close; plot( x,F(x), x,0*x )
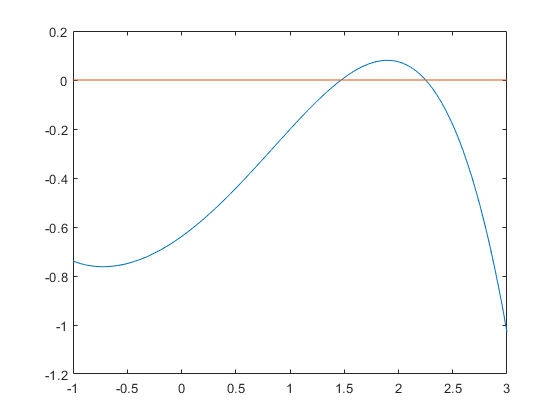
Plot the function including the x-axis

Hessians over ordinary intervals

The range of the function f and its first and second derivative over X=[1,2] is included by

X = infsup(1,2);
Yint = f(hessianinit(X))

intval Hessian value Yint.x = 
[  -0.87838452581391,   0.68131672798366] 
intval Hessian derivative(s) Yint.dx = 
[  -0.32071287481175,   0.56878121143607] 
intval Hessian second derivative(s) value Yint.hx = 
[  -1.38753101700004,   0.06347219524331]

Hessians over affine intervals

Better inclusions of the ranges may be computed by

Yaff = f(hessianinit(affari(X)))

affari Hessian value Yaff.x = 
[  -0.22166634434316,   0.20542612815224] 
affari Hessian derivative(s) Yaff.dx = 
[  -0.12197001939730,   0.53947300076961] 
affari Hessian second derivative(s) value Yaff.hx = 
[  -1.25805672986527,  -0.08729371200877]

For example, it becomes clear that the second derivative f" has no root in [1,2].

Zeros of a function

There are two roots near 1.5 and 2.5, and two extrema near -0.5 and 2. The roots can be included by verifynlss. For this simple function the inclusion is of maximum accuracy.

X1 = verifynlss(f,1.5)
X2 = verifynlss(f,2.5)

intval X1 = 
   1.47132336560595
intval X2 = 
   2.25002867328683

Extrema of a function

The extrema can be approximated and included using Hessians. The following is one step of a simple Newton iteration starting at x=-0.5 :

x = -0.5;
y = f(hessianinit(x));
x = x - y.hx\y.dx';
y

Hessian value y.x = 
  -0.749124828278367
Hessian derivative(s) y.dx = 
   0.113228338943107
Hessian second derivative(s) value y.hx = 
   0.468843719809578

Inclusion of extrema

Inclusions of the extrema of f are computed by verifylocalmin.

X1 = verifylocalmin(f,-0.5)
X2 = verifylocalmin(f,2)

intval X1 = 
  -0.72343012456517
intval X2 = 
                NaN

Functions in several unknowns

Function with several unknowns are handled in a similar manner. Consider the following test function by N. Gould. It is taken from the Coconut collection of test function for global optimization, http://www.mat.univie.ac.at/~neum/glopt/coconut/benchmark/Library2.html .

f = inline(' x(3)-1 + sqr(x(1)) + sqr(x(2)) + sqr(x(3)+x(4)) + sqr(sin(x(3))) +  sqr(x(1))*sqr(x(2)) + x(4)-3 + sqr(sin(x(3))) + sqr(x(4)-1) + sqr(sqr(x(2))) + sqr(sqr(x(3)) + sqr(x(4)+x(1))) + sqr(x(1)-4 + sqr(sin(x(4))) + sqr(x(2))*sqr(x(3))) + sqr(sqr(sin(x(4)))) ')

f =
     Inline function:
     f(x) = x(3)-1 + sqr(x(1)) + sqr(x(2)) + sqr(x(3)+x(4)) + sqr(sin(x(3))) +  sqr(x(1))*sqr(x(2)) + x(4)-3 + sqr(sin(x(3))) + sqr(x(4)-1) + sqr(sqr(x(2))) + sqr(sqr(x(3)) + sqr(x(4)+x(1))) + sqr(x(1)-4 + sqr(sin(x(4))) + sqr(x(2))*sqr(x(3))) + sqr(sqr(sin(x(4))))

Approximation of an extremum

On the Web-site the global minimum of that function in 4 unknowns is given as 5.7444 . We use a couple of a Newton iterations starting at x=ones(4,1) to approximate a stationary point:

format short
x = ones(4,1);
for i=1:20
   y = f(hessianinit(x));
   x = x - y.hx\y.dx';
end
x
y.dx

x =
    1.4599
         0
    0.0809
   -0.8111
ans =
   1.0e-15 *
    0.8882   -0.0000    0.1110   -0.8882

Now x is an approximation of a stationary point: The gradient of f evaluated at x is not too far from zero. Note that many iterations were necessary due to the poor quality of the initial approximation ones(4,1).

Inclusion of a stationary point

Using this approximation an inclusion of a stationary point of f is computed by (in this case the last parameter 1 is used to see intermediate results):

format long
X = verifylocalmin(f,x,[],1)

residual norm(f'(xs_k)), floating point iteration 1
ans =
     1.778307332460799e-15
residual norm(f'(xs_k)), floating point iteration 2
ans =
     9.945640348601413e-16
residual norm(f'(xs_k)), floating point iteration 3
ans =
     9.945640348601413e-16
interval iteration 1
intval X = 
   1.45986156438163
   0.00000000000000
   0.08089005653386
  -0.81111308458517

Inclusion of a minimum

The interval vector X includes a root of f', i.e. a stationary point xx of f. To prove that f has a minimum at xx we need to prove positive definiteness of the Hessian of f evaluated at xx. The interval vector X includes the stationary point xx of f. So we compute an inclusion Y of the Hessian at X.

Mathematically, for every x in X the following is true: Y.x is an inclusion of f(x), Y.dx is an inclusion of f'(x), and Y.hx is an inclusion of the Hessian of f at x. Especially, the Hessian of f evaluated at xx is included in Y.hx.

Y = f(hessianinit(X));
format _
Y.hx

intval ans = 
   9.0766678854428_   0.00000000000000   0.41981840965597   3.0793123311663_
   0.00000000000000   6.20966816386002   0.00000000000000   0.00000000000000
   0.41981840965597   0.00000000000000   7.7097852348661_   2.41981840965596
   3.0793123311663_   0.00000000000000   2.41981840965596  13.3722229587129_

This interval matrix contains obviously only diagonally dominant matrices, so the stationary point xx of f in X is indeed a (local) minimum.

A model problem in 5000 unknowns I

Consider the problem "bdqrtic" in

  Source: Problem 61 in
     A.R. Conn, N.I.M. Gould, M. Lescrenier and Ph.L. Toint,
     "Performance of a multifrontal scheme for partially separable optimization",
      Report 88/4, Dept of Mathematics, FUNDP (Namur, B), 1988.
      Copyright (C) 2001 Princeton University
      All Rights Reserved
  see bottom of file test_h.m

The model problem is

   N = length(x);      % model problem: N = 1000, initial approximation x=ones(N,1);
   I = 1:N-4;
   y = sum( (-4*x(I)+3.0).^2 + ( x(I).^2 + 2*x(I+1).^2 + ...
             3*x(I+2).^2 + 4*x(I+3).^2 + 5*x(N).^2 ).^2 );

This function is evaluated by

   index = 2;
   y = test_h(x,index);

A model problem in 5000 unknowns II

The given starting vector is x = ones(5000,1). Recall that y = f(hessianinit(x)) has 5000 elements in y.x, 2.5e7 elements in y.dx and 1.25e11 elements in y.hx. In full storage this would mean 1 TeraByte of storage.

The following calculates an inclusion of a stationary point of f by first performing a simple Newton iteration followed by a verification step for the nonlinear system. The Hessian is treated as full matrix, so the computation may take a while.

n = 5000;
index = 2;
tic
X = verifylocalmin('test_h',ones(n,1),[],1,index);
tfull = toc
max(relerr(X))

residual norm(f'(xs_k)), floating point iteration 1
ans =
     1.499415844035270e+06
residual norm(f'(xs_k)), floating point iteration 2
ans =
     4.442651106586590e+05
residual norm(f'(xs_k)), floating point iteration 3
ans =
     1.316745943265305e+05
residual norm(f'(xs_k)), floating point iteration 4
ans =
     3.902878013156914e+04
residual norm(f'(xs_k)), floating point iteration 5
ans =
     1.008486090604475e+04
residual norm(f'(xs_k)), floating point iteration 6
ans =
     9.990290941444042e+02
residual norm(f'(xs_k)), floating point iteration 7
ans =
  17.085974829564289
residual norm(f'(xs_k)), floating point iteration 8
ans =
   0.070681934486502
residual norm(f'(xs_k)), floating point iteration 9
ans =
   0.003385440115388
residual norm(f'(xs_k)), floating point iteration 10
ans =
     2.846875081065139e-06
residual norm(f'(xs_k)), floating point iteration 11
ans =
     2.594087847144787e-13
interval iteration 1
interval iteration 2
tfull =
   8.402818773730102
ans =
     5.993402063076835e-16

A model problem in 5000 unknowns III

Note the small maximum relative error of the inclusion of the result. Verification is faster when solving the nonlinear system treating the Hessian as sparse. This is done by the following.

n = 5000;
index = 2;
tic
X = verifylocalmin('test_h',ones(n,1),'SparseSPD',1,index);
tsparse = toc
tfull
maxrelerrX = max(relerr(X))

residual norm(f'(xs_k)), floating point iteration 1
ans =
     1.499415844035270e+06
residual norm(f'(xs_k)), floating point iteration 2
ans =
     4.442651106586590e+05
residual norm(f'(xs_k)), floating point iteration 3
ans =
     1.316745943265305e+05
residual norm(f'(xs_k)), floating point iteration 4
ans =
     3.902878013156914e+04
residual norm(f'(xs_k)), floating point iteration 5
ans =
     1.008486090604475e+04
residual norm(f'(xs_k)), floating point iteration 6
ans =
     9.990290941444042e+02
residual norm(f'(xs_k)), floating point iteration 7
ans =
  17.085974829564289
residual norm(f'(xs_k)), floating point iteration 8
ans =
   0.070681934486502
residual norm(f'(xs_k)), floating point iteration 9
ans =
   0.003385440115388
residual norm(f'(xs_k)), floating point iteration 10
ans =
     2.846875081065139e-06
residual norm(f'(xs_k)), floating point iteration 11
ans =
     2.594087847144787e-13
interval iteration 1
interval iteration 2
tsparse =
   0.742086367547861
tfull =
   8.402818773730102
maxrelerrX =
     8.648169949349551e-14

Note that verification is faster at the price of a less narrow inclusion (for comparison the previous time tfull is displayed).

Verification of a minimum

The solution X is already proved to include a (local) minimum. To verify that, the Hessian at X is computed which includes in particular the Hessian at the stationary point xhat in X.

y = test_h(hessianinit(X),index);
isspd(y.hx)

ans =
  logical
   1

Then the interval Hessian is proved by "isspd" to be symmetric positive definite: Mathematically the result "isspd(M)=1" for a symmetric (Hermitian) interval matrix M proves that every symmetric (Hermitian) matrix A within M is positive definite. In our case in particular the Hermitian of f at the stationary point xhat. Therefore, xhat is proved to be a local minimum of f.

Enjoy INTLAB

INTLAB was designed and written by S.M. Rump, head of the Institute for Reliable Computing, Hamburg University of Technology. Suggestions are always welcome to rump (at) tuhh.de


Published with MATLAB® R2020a