| Home |
 |
Download |
 |
Publikationen |
 |
Second-Order PMD-Compensation |
|
.
Component for Second-Order Compensation of Polarization-Mode Dispersion
Jörn Patscher and Ralf Eckhardt
Technical University Hamburg-Harburg, 21071 Hamburg, Germany
April 1997
The Compensation of polarization-mode dispersion in long
fibers by using principal states of polarization
is limited in bandwidth, when
these states vary with frequency.
We characterize a compensator,
containing high birefringent fibers and
polarization controllers,
which is adapted to these variation and
promises enlarged bandwidth.
This work is also published in Electronics Letters [5]
and reproduced here by kind permission of the
IEE.
A Postscript file is available for downloading and printing.
We do also provide more information about our group
Optics and Instrumentation.
See also our
Publication List.
Introduction
Polarization-mode dispersion (PMD)
remains the dominant
bitrate-limiting effect in long single mode (SM) fibers,
when chromatic dispersion is reduced by
state-of-the-art techniques like
compensating fibers or chirped gratings.
Recently published techniques for PMD compensation
[1]
are based on
splitting the signal after transmission into two parts,
which are aligned with either of the two
principal states of polarization (PSP) of the fiber.
Each part on its own does not suffer from PMD in first order approximation,
but has undergone different group delays.
The differential group delay (DGD) may be equalized as shown in
Fig.1
by launching the fast signal part into the slow eigenstate
of a polarization maintaining (PM) high birefringent fiber
and vice versa.
This approach works well as long as
the PSP of the compensator
(i.e. the combination of polarization controller (PC) and PM fiber)
matches to the PSP of the SM fiber,
but residual DGD appears due to misalignment, if
the PSP's vary with the signal wavelength.
Taking e.g. the data from [2],
the PSP variation in a 147km long cable
would restrict the bandwidth,
which could be covered simultaneously by this compensation method,
to roughly 10-100 GHz.
Considering now transcontinental cable lengths,
wavelength multiplexing, and
future multigigabitrates,
PMD compensation
will require close approximation of the PSP's of
SM fiber and compensator PSP over a larger bandwidth,
i.e. the 1st-order approach of treating the
compensator PSP as constant
must be extended to PSP's, which are
linear or higher order function of frequency.
Here, we theoretically and experimentally describe a compensator,
which provides linear PSP variation.
Principle of Operation
The components of a PMD compensation setup (Fig.1)
can be described compactly by
polarization dispersion vectors [2],
which point to the PSP's on the Poincaré sphere [3]
and indicate the DGD by their lengths.
Then it can be shown, that
the residual DGD after compensation
(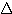 t)
can be expressed as vectorial sum
t)
can be expressed as vectorial sum
| | 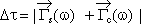 | (1) |
where
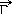 s and
s and
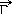 c are
the PSP vectors of the SM fiber and the compensator
at their connection (A).
Both are generally functions of frequency w.
Assuming good compensation at an arbitrarily chosen center frequency w0,
(i.e.
c are
the PSP vectors of the SM fiber and the compensator
at their connection (A).
Both are generally functions of frequency w.
Assuming good compensation at an arbitrarily chosen center frequency w0,
(i.e. 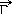 s(w0)
s(w0)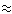 -
-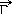 c(w0)),
a taylor series expansion yields the residual
DGD at frequency deviations
c(w0)),
a taylor series expansion yields the residual
DGD at frequency deviations
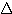 w=w-w0
as
w=w-w0
as
| | 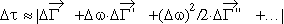 | (2) |
with
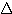
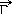
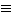
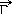 s-(-
s-(-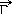 c)
and the symbols (') and ('') denoting the 1st and 2nd
derivatives with respect to w, taken at w0.
A first-order compensation, as indicated in Fig.1,
provides
c)
and the symbols (') and ('') denoting the 1st and 2nd
derivatives with respect to w, taken at w0.
A first-order compensation, as indicated in Fig.1,
provides
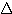
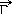 (w0)=
(w0)=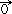 and
leaves a finite 1st-order term
and
leaves a finite 1st-order term
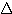
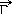 ',
which causes the DGD to grow linearly with
',
which causes the DGD to grow linearly with
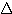 w.
Further minimization of
w.
Further minimization of
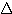 t(w) can be achieved by
additionally cancelling this 1st-order term
(
t(w) can be achieved by
additionally cancelling this 1st-order term
(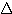
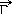 '=
'=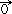 ), as is
provided by an extended 2nd-order compensator (Fig.2).
Here, a PSP variation rate
), as is
provided by an extended 2nd-order compensator (Fig.2).
Here, a PSP variation rate
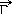 'c is
introduced, which is subject of the following analysis.
'c is
introduced, which is subject of the following analysis.
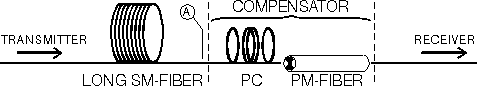
Fig.1: Single-Stage PMD Compensation
The fast PSP of the long SM-fiber
at (A) is aligned
to the slow axis of the PM-fiber by the
polarization controller (PC) and vice versa.
Fig.2: Experimental Setup
LASER = Erbium-Ringlaser (1525-1570nm),
P=Polarizer, PC1,PC2 = Polarization Controllers, PM#1, #2 = 2.00m and 1.15m
length of PM fibers (Fujikura SM6/150, Bow-Tie),
t1=1.58 ps, t2=0.91ps.
PM#1 and PM#2 were temporarily arranged in reversed order.
In a real system, the arrangement between (A) and (B) would replace the single
PM-fiber in fig.1..
Theoretical Analysis
The PSP and the DGD of the core of the compensator,
i.e. the components between (A) and (B) in Fig.2,
are to be calculated.
Each part of the setup can be characterized by
a unitary Jones matrix Ji:
| | 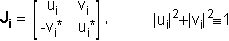 | (3) |
where
i={1,2,PC2,c}
indicates the PM fibers PM#1 and PM#2, PC2, and
the combination of them, given by
Jc=J2×JPC2×J1.
The transformation properties of PC1 and PC2
are assumed
not to depend significantly on frequency, so, using eqn.3,
the elements of JPC2
can be noted generally as
| | 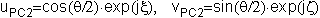 | (4) |
where
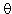 denotes the angular distance
on the Poincaré sphere
between the slow eigenstate of the first PM fiber and
the State of Polarisation (SOP), to which this eigenstate
is transformed by PC2.
As PC1 would contribute just a left-multiplication
with a constant matrix, it is omitted here.
The PM fibers are characterized by
denotes the angular distance
on the Poincaré sphere
between the slow eigenstate of the first PM fiber and
the State of Polarisation (SOP), to which this eigenstate
is transformed by PC2.
As PC1 would contribute just a left-multiplication
with a constant matrix, it is omitted here.
The PM fibers are characterized by
| | 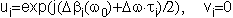 | (5) |
where t1,2 are the DGD, which were experimentally
verified to have negligible variations within the used bandwidth,
and
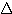
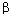 1,2
are the mean differential phase delays.
An eigenvalue analysis
of Jc(w),
which is given in detail e.g. in [4],
now yields the total DGD (tc) of the compensator,
1,2
are the mean differential phase delays.
An eigenvalue analysis
of Jc(w),
which is given in detail e.g. in [4],
now yields the total DGD (tc) of the compensator,
| | 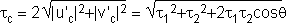 | (6) |
and the slow input PSP (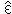 a+):
a+):
| | 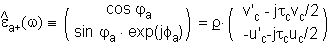 | (7) |
where
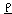 represents a common phase and amplitude.
The angels
represents a common phase and amplitude.
The angels
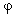 a and
a and
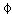 a identify coordinates
on the Poincaré sphere, as indicated in Fig.3b, and will be
expressed explicitly
in eqn.8 and eqn.9.
As a result of the symmetrical structure
of the setup between (A) and (B),
the corresponding expressions for the output PSP
(
a identify coordinates
on the Poincaré sphere, as indicated in Fig.3b, and will be
expressed explicitly
in eqn.8 and eqn.9.
As a result of the symmetrical structure
of the setup between (A) and (B),
the corresponding expressions for the output PSP
(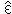 b+,
b+,
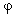 b and
b and
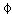 b)
at (B)
can be obtained from eqn.7
by exchanging the terms
u1,2 against u2,1,
which are implicitly contained in uc' and vc'.
A straightforward calculation yields:
b)
at (B)
can be obtained from eqn.7
by exchanging the terms
u1,2 against u2,1,
which are implicitly contained in uc' and vc'.
A straightforward calculation yields:
| | 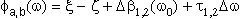 | (8) |
and
| | 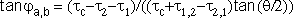 | (9) |
These Eqn's. describe
a circular variation of the compensator PSP
on the Poincaré sphere (Fig.3b).
The radius ra,b=|sin2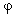 a,b|,
the DGD (tc), and also
the PSP variation rate
(|
a,b|,
the DGD (tc), and also
the PSP variation rate
(|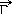 'c/tc| = t1×ra)
are fully determined by the same set of three parameters,
(t1, t2 and
'c/tc| = t1×ra)
are fully determined by the same set of three parameters,
(t1, t2 and 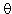 )
and thus do not depend on frequency.
Modification of the parameters
)
and thus do not depend on frequency.
Modification of the parameters
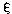 ,
,
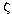 or
or
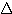
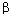 i has the same effect as
applying a frequency offset
i has the same effect as
applying a frequency offset
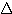 w.
The first PC, which has been ignored so far, provides for
w.
The first PC, which has been ignored so far, provides for
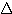
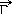 (w0)=
(w0)=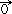 and
and
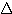
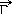 '(w0)=
'(w0)=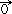 by transforming the input PSP of the compensator
to any arbitrary position and by
also controlling the
variation direction
by transforming the input PSP of the compensator
to any arbitrary position and by
also controlling the
variation direction
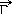 'c(w0)/tc,
while the variation rate |
'c(w0)/tc,
while the variation rate |
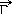 'c| is
controlled by PC2.
'c| is
controlled by PC2.
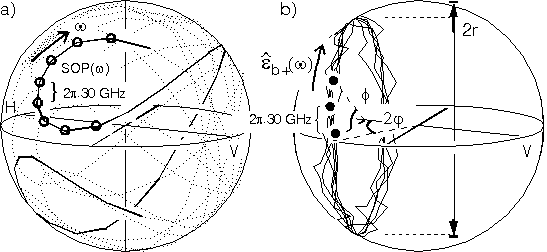 Fig.3: Poincare representation
Fig.3: Poincare representation
a) Sample trajectory of output SOP at (B)
while frequency sweeping.
Circles (o): measured SOP's in steps of 30 GHz
(not all shown).
Solid part of the line: Frequency interval 900 GHz.
b) PSP at (B), determined from SOP's.
Angular coordinates according to eqn.7.
2r=diameter of PSP trajectory.
Experimental
Some assumptions about component properties were used
in Eqn's (4) and (5),
so for experimental verification
of the Eqn's (8) and (9),
a compensator was set up and characterized (Fig.2).
The DGD and the PSP were analyzed
by sweeping the input wavelength
by
 w
w 36 THz
from 1525 to 1570 nm
and monitoring
the output SOP trajectory (Fig.3a)
at various settings of PC1 and
PC2.
Local rotation axes of the SOP were identified
for determination of the DGD (tc)
and the PSP (
36 THz
from 1525 to 1570 nm
and monitoring
the output SOP trajectory (Fig.3a)
at various settings of PC1 and
PC2.
Local rotation axes of the SOP were identified
for determination of the DGD (tc)
and the PSP ( b, Fig.3b).
The DGD was found to be independent of frequency
within 2% measurement accuracy, while
the PSP exhibited
the predicted circular variation.
The slope of the phase
b, Fig.3b).
The DGD was found to be independent of frequency
within 2% measurement accuracy, while
the PSP exhibited
the predicted circular variation.
The slope of the phase
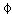 b of the circular variation (Fig.4a)
agrees closely to eqn.8.
The corresponding PSP variation at the input (A),
was obtained by exchanging the two HiBi-fibers against each other.
The slope of the measured circulation phase
b of the circular variation (Fig.4a)
agrees closely to eqn.8.
The corresponding PSP variation at the input (A),
was obtained by exchanging the two HiBi-fibers against each other.
The slope of the measured circulation phase
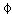 a meets
eqn.8 within 3%.
As
a meets
eqn.8 within 3%.
As
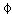 (w0) was arbitrarily
set to zero due to technical reasons,
no information about
(w0) was arbitrarily
set to zero due to technical reasons,
no information about
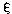 ,
,
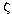 ,
or
,
or
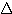
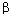 (w0)
could be obtained.
Finally (Fig.4b)
the measured circulation radii ra,b
were compared
to calculated values
from eqn.9.
The setting of
(w0)
could be obtained.
Finally (Fig.4b)
the measured circulation radii ra,b
were compared
to calculated values
from eqn.9.
The setting of
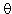 , which is used in eqn.9,
was obtained from
measured values
of the total DGD (tc)
by reverse evaluation of eqn.6.
, which is used in eqn.9,
was obtained from
measured values
of the total DGD (tc)
by reverse evaluation of eqn.6.
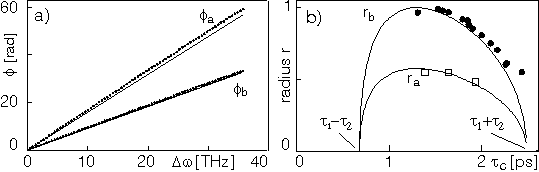
Fig.4: Experimental results
a) Phase of the PSP circulation
at the output and at input.
Solid lines: predicted from eqn.8, dots: measured.
b) Radii ra,b of PSP circulation
vs. total DGD tc( ).
Dots: measured at port (B),
squares: measured at (A),
solid lines: predicted from eqn.9.
).
Dots: measured at port (B),
squares: measured at (A),
solid lines: predicted from eqn.9.
Conclusion
As experimentally verified,
the above described compensator allows for
PMD compensation within a frequency interval, where
the PSP trajectory of the communication fiber
can be approximated by a single arc on the Poincaré sphere.
Compensation of variations of the DGD
will require one further compensator stage.
However, the effect of PSP variation
is expected to dominate the latter [2], so,
compared to single-stage (1st order) compensators [1],
this setup promises substantial increase
of bitrate and/or repeater distance in multigigabit systems.
Acknowledgement
The authors wish to thank R.Ulrich and E.Brinkmeyer
for fruitful discussions during this investigation
and
H. Rosenfeldt
for great technical support.
References
| [1] |
B.W.Hakki:
"Polarization Mode Dispersion Compensation by Phase Diversity Detection",
IEEE Photonics Technology Letters, 9, pp.121-123, 1997 ;
|
| [2] |
C.D.Poole, N.S.Bergano, R.E.Wagner, and H.J.Schulte:
"Polarization Dispersion and Principal States in a 147-km Undersea Lightwave Cable",
Journal of Lightwave Technology, LT-6, pp.1185-1191, 1988 ;
|
| [3] |
A.Simon and R.Ulrich :
"Evolution of Polarization along a single-mode fiber",
Applied Physics Letters, 31, pp.517-520, 1977 ;
|
| [4] |
C.D.Poole and R.E.Wagner:
"Phenomenological approach to polarization dispersion in long single-mode fibers",
Electronics Letters, 22, pp.1029-1030, 1986 ;
|
| [5] |
J.Patscher and R.Eckhardt:
"Component for second-order compensation of polarisation-mode dispersion",
Electronics Letters, 33, pp.1157-1159, 1997 ;
|
You may find further information in our
Publication List.
More about Polarization can be found at our
Polarization and Birefringence Page.






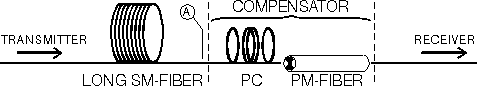
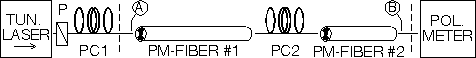


 Home
Home  rosenfeldt@tu-harburg.de
rosenfeldt@tu-harburg.de